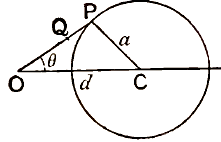
Let O be taken as pole and the line through the centre C as the initial line. Let OC = d, and let the radius of the circle be a.
The equation to the circle is then
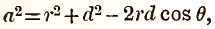
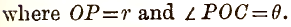
Let OQ be p, so that, by the given condition,
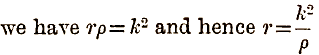
Substituting this value in the equation to the circle, we have
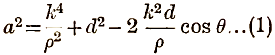
so that the equation to the locus of Q is
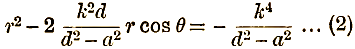
But the equation to a circle, whose radius is a' and whose centre is on the initial line at a distance d', is
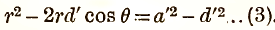
Comparing (1) and (2), we see that the required locus is a circle, such that
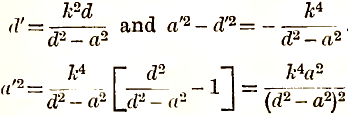
The required locus is therefore a circle, of radius
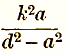
whose centre is on the same line as the original centre at a distance
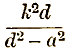
from the fixed point.
When **** on the original circle the distance d is equal to a, and the equation (1) becomes k2 = 2dr cos θ i.e., in Cartesian coordinates,
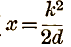
In this case the required locus is a straight line perpendicular to OC.
When a second curve is obtained from a given curve by the above geometrical process, the second curve is said to be the inverse of the first curve and the fixed point O is called the centre of inversion.
The inverse of a circle is therefore a circle or a straight line according as the centre of inversion is not, or is, on the circumference of the original circle.