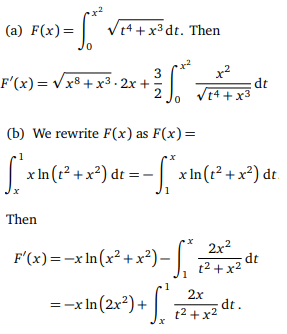Question

Differentiating under the integral. Under mild continuity restrictions, it is true that if

F(x) = ∫g(t, x) t∈[a,b] dt

than f'(x)=∫gx (t,x) t∈[a,b] dt.using this fact and the chain rule we can find the derivities of

f(x)= ∫g(t, x) t∈[afx]dt

by letting

G(u, x) =∫ g(t, x) t∈[au]dt

where u = f (x). Find the derivatives of the following functions

(a) F(x) =∫ t∈ √t 4 + x 3 [dt]

(b) F(x) =∫ t∈x ln(t 2 + x 2 )[dt]

Answer 1

With G(u, x) defined as above we have

F(x) = G(f (x), x)

and we can find the derivative of F using the chain rule

F'(x) = Gu(f (x), x)f'(x) + Gx (f (x), x)

We know from the problem statement, that

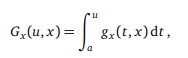
and what we need know is the derivative Gu (u, x). But this we obtain from the fundamental theorem of calculus, which states that

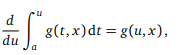
or in our notation, Gu (u, x) = g(u, x). It means that differentiating an integral with respect to the upper limit results in the function we are integrating. Putting it all together we obtain

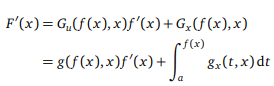
Now we are ready to attempt the problems