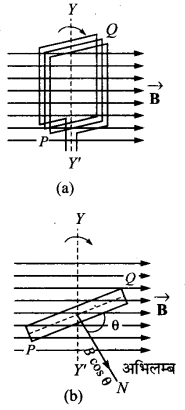
माना एक कुण्डली के तल का क्षेत्रफल A है तथा इसमें तार के N फेरे हैं। इस कुण्डली को एक नियत कोणीय वेग ω से चित्र (a) की भाँति एक ऊर्ध्वाधर अक्ष YY’ के परितः एकसमान चुम्बकीय क्षेत्र B में दक्षिणावर्त दिशा में घुमाया जा रहा है।
माना किसी क्षण कुण्डली के तल पर खींचा गया अभिलम्ब अर्थात् कुण्डली का अक्ष चित् (b) की भाँति Vector B की दिशा के साथ θ कोण बनाता है। इस क्षण चुम्बकीय क्षेत्र B का कुण्डली के तल के लम्बवत् घटक B cosθ से होगा।

e = NBAω sinωt …(1)
प्रेरित वि० वी० बल के लिए सूत्र (1) से स्पष्ट है कि प्रेरित वि० वा० बल का मान समय t के साथ-साथ निरन्तर बदलता रहेगा परन्तु sinωt का अधिकतम मान 1 होता है। अतः प्रेरित विद्युत वाहक बल e का अधिकतम मान = NBAω होगा। यदि इसको e0 से प्रदर्शित किया जाए तो प्रेरित विद्युत वाहक बल के लिए सूत्र (1) को निम्नलिखित रूप में व्यक्त किया जाता है।
e = e0 sinωt …(2)
जहाँ e का अधिकतम मान e0 = NBAω उपर्युक्त सूत्र (2) से स्पष्ट है कि जब किसी कुण्डली को चुम्बकीय क्षेत्र में घुमाया जाता है तो उसमें प्रेरित विद्युत वाहक बल उत्पन्न हो जाता है जो ज्या-वक्र (sine curve) की भाँति बदलता रहता है। इसका मान कुण्डली के घुमाव कोण θ = ωt पर निर्भर करता है।
जब कुण्डली का तल चुम्बकीय क्षेत्र के लम्बवत् होता है तब से θ = 0°
अतः e = e0 sin 0° = 0
अर्थात् e का मान शून्य होता है। यह कुण्डली की प्रारम्भिक स्थिति है तथा प्रत्येक चक्कर के पश्चात् यही स्थिति होती है। जब कुण्डली चौथाई चक्कर घूम जाती है तो θ = 90°
तथा इस दशा में e = e0 sin 90° = e0 (अधिकतम)
यही स्थिति कुण्डली के तीन-चौथाई चक्कर घूमने पर आती है परन्तु विपरीत दिशा में प्रेरित विद्युत वाहक बल अधिकतम होता है।
अर्थात् e = – e0
इस प्रकार कुण्डली के पहले आधे चक्कर में कुण्डली में उत्पन्न प्रेरित वि० वी० बल शून्य से बढ़कर अधिकतम मान को प्राप्त करता है तथा पुनः घटकर शून्य हो जाता है, जबकि शेष आधे चक्कर में यह विपरीत दिशा में अधिकतम मान को प्राप्त करता है तथा पुनः घटकर शून्य हो जाता है। यही क्रिया बार-बार दोहरायी जाती है।