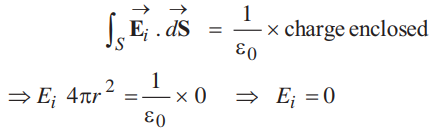Electric field intensity at a point outside a uniformly charged thin spherical shell: Consider a uniformly charged thin spherical shell of radius R carrying charge Q. To find the electric field outside the shell, we consider a spherical Gaussian surface of radius r (>R), concentric with given shell. If vector E is electric field outside the shell, then by symmetry electric field strength has same magnitude E0 on the Gaussian surface and is directed radially outward. Also the directions of normal at each point is radially outward, so angle between vector Ei and d vector * is zero at each point. Hence, electric flux
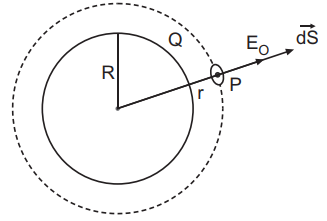

Now, Gaussian surface is outside the given charged shell, so charge enclosed by Gaussian surface is Q.
Hence, by Gauss'* theorem
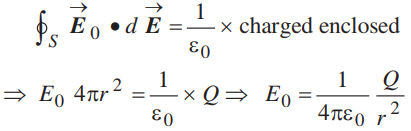
Thus, electric field outside a charged thin spherical shell is the same as if the whole charge Q is concentrated at the centre.
If σ is the surface charge density of the spherical shell, then
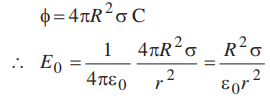
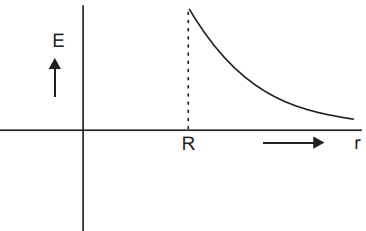
Electric field inside the shell (hollow charged conducting sphere): The charge resides on the surface of a conductor. Thus a hollow charged conductor is equivalent to a charged spherical shell. To find the electric field inside the shell, we consider a spherical Gaussian surface of radius r (< R), concentric with the given shell. If vector E is the electric field inside the shell, then by symmetry electric field strength has the same magnitude Ei on the Gaussian surface and is directed radially outward. Also the directions of normal at each point is radially outward, so angle between vector Ei and d vector * is zero at each point. Hence, electric flux through Gaussian surface
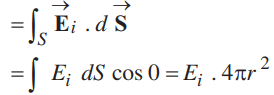
Now, Gaussian surface is inside the given charged shell, so charge enclosed by Gaussian surface is zero.
Hence, by Gauss’* theorem